Cells and Cancer in Python



















import matplotlib.pyplot as plt

import numpy as np


# Plot 1: Order Parameter vs Time (S vs t)

t = np.linspace(0, 10, 500)

S = 1 / (1 + np.exp(-2 * (t - 5)))  # sigmoid rise

plt.figure()

plt.plot(t, S)

plt.title("Order Parameter S vs Time")

plt.xlabel("Time (t)")

plt.ylabel("Order Parameter (S)")

plt.grid(True)

plt.show()


# Plot 2: Energy Collapse

E = np.maximum(0, 1 - 0.1 * t**1.5)

plt.figure()

plt.plot(t, E, color='red')

plt.title("Cellular Energy (E) Collapse Over Time")

plt.xlabel("Time (t)")

plt.ylabel("Energy (E)")

plt.grid(True)

plt.show()


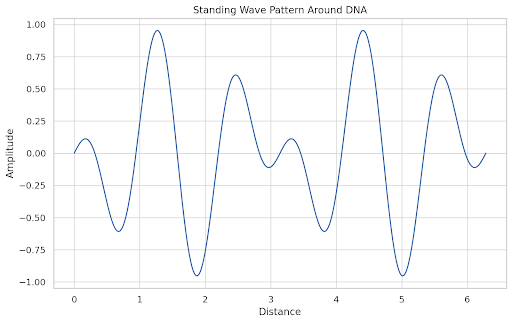
# Plot 3: Standing Wave Stability

x = np.linspace(0, 2*np.pi, 500)

standing_wave = np.sin(x) * np.cos(5 * x)

plt.figure()

plt.plot(x, standing_wave)

plt.title("Standing Wave Pattern Around DNA")

plt.xlabel("Distance")

plt.ylabel("Amplitude")

plt.grid(True)

plt.show()


# Plot 4: DNA Repair Rate vs Redox State

redox = np.linspace(0, 1, 100)

repair_rate = redox**2

plt.figure()

plt.plot(redox, repair_rate)

plt.title("DNA Repair Rate vs Redox State")

plt.xlabel("Redox State (R)")

plt.ylabel("Repair Rate")

plt.grid(True)

plt.show()


# Plot 5: Phase Space of Cell State

H, E = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))

S = H * E

plt.figure()

plt.contourf(H, E, S, levels=20, cmap='viridis')

plt.title("Phase Space of Order Parameter S(H, E)")

plt.xlabel("Hydration (H)")

plt.ylabel("Energy (E)")

plt.colorbar(label="Order Parameter S")

plt.show()


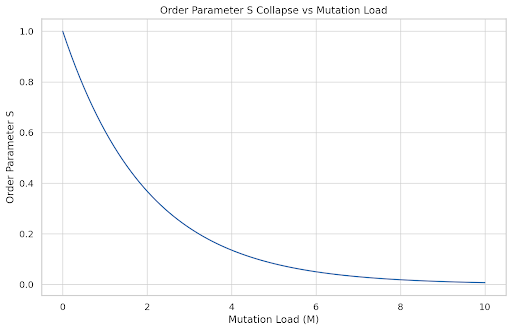
# Plot 6: Cell Collapse Threshold

M = np.linspace(0, 10, 100)

S_threshold = np.exp(-0.5 * M)

plt.figure()

plt.plot(M, S_threshold)

plt.title("Order Parameter S Collapse vs Mutation Load")

plt.xlabel("Mutation Load (M)")

plt.ylabel("Order Parameter S")

plt.grid(True)

plt.show()












 import matplotlib.pyplot as plt

import numpy as np


# Plot 7: Epigenetic Noise vs Environmental Stability

env_stability = np.linspace(0, 1, 100)

epigenetic_noise = 1 / (env_stability + 0.01)


plt.figure(figsize=(6, 4))

plt.plot(env_stability, epigenetic_noise, color='darkred')

plt.title("Epigenetic Noise vs Environmental Stability")

plt.xlabel("Environmental Stability (normalized)")

plt.ylabel("Epigenetic Noise (arbitrary units)")

plt.grid(True)

plt.tight_layout()

plt.show()


# Plot 8: Impedance Spectra of Cellular Order (mock frequency vs phase)

freq = np.logspace(0, 3, 100)

impedance = 1 / np.sqrt(1 + (freq / 10)**2)

phase_shift = -np.arctan(freq / 10)


plt.figure(figsize=(6, 4))

plt.semilogx(freq, phase_shift, label='Phase Shift', color='purple')

plt.title("Cellular Impedance Phase vs Frequency")

plt.xlabel("Frequency (Hz)")

plt.ylabel("Phase Shift (radians)")

plt.grid(True, which='both')

plt.tight_layout()

plt.show()


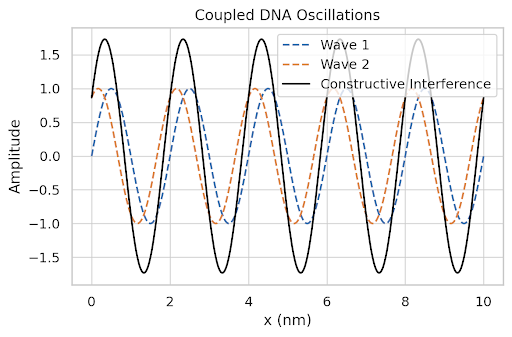
# Plot 9: Coupled DNA Wave Function Interference

x = np.linspace(0, 10, 500)

wave1 = np.sin(2 * np.pi * 0.5 * x)

wave2 = np.sin(2 * np.pi * 0.5 * x + np.pi / 3)

combined = wave1 + wave2


plt.figure(figsize=(6, 4))

plt.plot(x, wave1, '--', label='Wave 1')

plt.plot(x, wave2, '--', label='Wave 2')

plt.plot(x, combined, label='Constructive Interference', color='black')

plt.title("Coupled DNA Oscillations")

plt.xlabel("x (nm)")

plt.ylabel("Amplitude")

plt.legend()

plt.grid(True)

plt.tight_layout()

plt.show()


# Plot 10: Phase Transition Triggered by Temperature Rise

T = np.linspace(36, 42, 100)

S = 1 / (1 + np.exp(5 * (T - 39)))


plt.figure(figsize=(6, 4))

plt.plot(T, S, color='green')

plt.title("Order Parameter Collapse via Temperature")

plt.xlabel("Temperature (°C)")

plt.ylabel("Cellular Order Parameter (S)")

plt.grid(True)

plt.tight_layout()

plt.show()






import matplotlib.pyplot as plt

import numpy as np

import seaborn as sns

import pandas as pd

import random

from sklearn.decomposition import PCA

from sklearn.preprocessing import StandardScaler

from sklearn.datasets import make_blobs

from mpl_toolkits.mplot3d import Axes3D

import ace_tools as tools


# Simulate cell type data with 6 environmental/biophysical features: 

# Hydration (H), Ion gradient (I), Energy availability (E), Redox potential (R), Chromatin order (C), Thermal stress (T)

cell_types = [

    "Neuron", "Cardiomyocyte", "Hepatocyte", "Beta Cell",

    "Skin Epithelial", "Hematopoietic Stem Cell", "Macrophage",

    "Fibroblast", "Adipocyte", "Osteocyte", "T-cell", "B-cell"

]


n_cells = len(cell_types)

features = ["Hydration", "Ion Gradient", "Energy", "Redox", "Chromatin Order", "Thermal Stress"]

n_features = len(features)


# Random but reasonable synthetic data for each cell type

np.random.seed(42)

data = np.clip(np.random.normal(loc=0.5, scale=0.15, size=(n_cells, n_features)), 0, 1)

df = pd.DataFrame(data, columns=features)

df["Cell Type"] = cell_types


# 3D PCA projection

scaler = StandardScaler()

scaled_data = scaler.fit_transform(df[features])

pca = PCA(n_components=3)

pca_result = pca.fit_transform(scaled_data)


fig = plt.figure(figsize=(10, 7))

ax = fig.add_subplot(111, projection='3d')

colors = sns.color_palette("hsv", n_cells)


for i, cell in enumerate(cell_types):

    ax.scatter(pca_result[i, 0], pca_result[i, 1], pca_result[i, 2], color=colors[i], label=cell, s=60)


ax.set_title("3D PCA of Biophysical Profiles of Human Cell Types")

ax.set_xlabel("PC1")

ax.set_ylabel("PC2")

ax.set_zlabel("PC3")

ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left')

plt.tight_layout()


tools.display_dataframe_to_user(name="Cell Biophysical Profiles", dataframe=df)


plt.show()














import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

from sklearn.decomposition import PCA


# Manually recreate the DataFrame for modeling cell types

data = {

    "Cell_Type": ["Neuron", "Hepatocyte", "Cardiomyocyte", "Pancreatic Beta Cell", "Epithelial Cell", "Hematopoietic Stem Cell"],

    "Hydration_H": [0.9, 0.7, 0.8, 0.85, 0.75, 0.88],

    "Ion_Concentration_I": [0.8, 0.75, 0.7, 0.85, 0.8, 0.9],

    "Energy_E": [0.9, 0.8, 0.85, 0.95, 0.7, 0.92],

    "Redox_R": [0.85, 0.8, 0.75, 0.9, 0.65, 0.9],

    "Crowding_C": [0.75, 0.9, 0.85, 0.7, 0.8, 0.78]

}


df = pd.DataFrame(data)


# Plot each cell type individually using raw features

import seaborn as sns

import matplotlib.pyplot as plt

import ace_tools as tools


for index, row in df.iterrows():

    values = row[1:].values.astype(float)

    labels = row.index[1:]

    

    plt.figure(figsize=(8, 5))

    sns.barplot(x=labels, y=values, palette="viridis")

    plt.ylim(0, 1)

    plt.title(f"{row['Cell_Type']} Biophysical Profile")

    plt.ylabel("Normalized Feature Value")

    plt.xlabel("Biophysical Features")

    plt.grid(True)

    plt.tight_layout()

    plt.show()















import matplotlib.pyplot as plt

import numpy as np

import pandas as pd

import seaborn as sns

from IPython.display import display


# Define cell types and biophysical parameters

cell_types = [

    "Hematopoietic Stem Cell", "Pancreatic Beta Cell", "Neuron",

    "Epithelial Cell", "Hepatocyte", "Cardiomyocyte"

]


# Normal state values (H, I, E, R, C)

normal_values = np.array([

    [0.8, 0.85, 0.9, 0.88, 0.75],  # HSC

    [0.7, 0.75, 0.95, 0.85, 0.7],   # Beta

    [0.9, 0.9, 0.85, 0.95, 0.6],    # Neuron

    [0.65, 0.7, 0.75, 0.7, 0.9],    # Epithelial

    [0.85, 0.8, 0.8, 0.7, 0.75],    # Hepatocyte

    [0.88, 0.9, 0.9, 0.85, 0.65]    # Cardiomyocyte

])


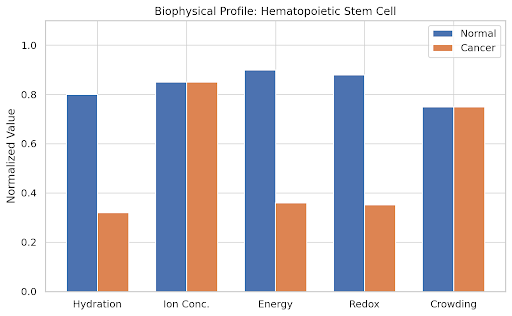
# Cancer state as a collapse in hydration, energy, and redox

cancer_values = normal_values.copy()

cancer_values[:, [0, 2, 3]] *= 0.4  # Reduce H, E, R


# Plotting

params = ['Hydration', 'Ion Conc.', 'Energy', 'Redox', 'Crowding']

x = np.arange(len(params))

width = 0.35


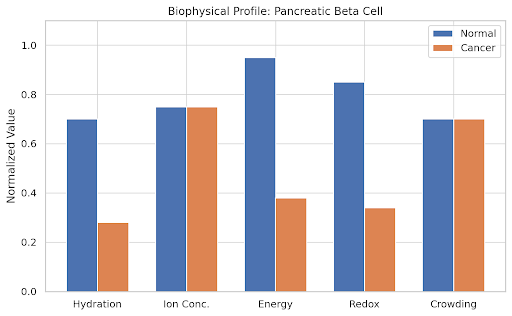
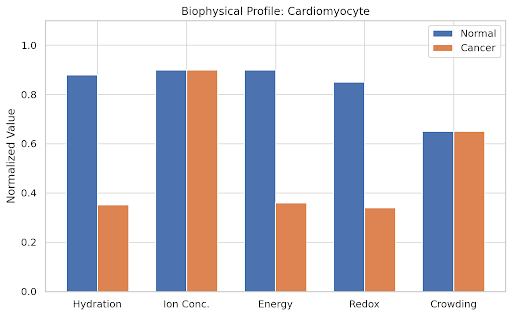
for i, cell in enumerate(cell_types):

    fig, ax = plt.subplots(figsize=(8, 5))

    ax.bar(x - width/2, normal_values[i], width, label='Normal')

    ax.bar(x + width/2, cancer_values[i], width, label='Cancer')

    ax.set_ylabel('Normalized Value')

    ax.set_title(f'Biophysical Profile: {cell}')

    ax.set_xticks(x)

    ax.set_xticklabels(params)

    ax.set_ylim(0, 1.1)

    ax.legend()

    plt.tight_layout()

    plt.show()




import matplotlib.pyplot as plt

import numpy as np


# Parameters representing normal neuronal state

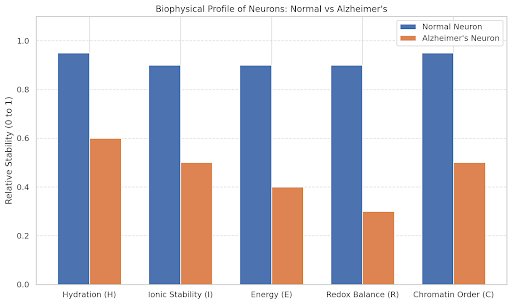
labels = ['Hydration (H)', 'Ionic Stability (I)', 'Energy (E)', 'Redox Balance (R)', 'Chromatin Order (C)']

normal = np.array([0.95, 0.9, 0.9, 0.9, 0.95])


# Parameters representing Alzheimer’s-affected neurons

alzheimers = np.array([0.6, 0.5, 0.4, 0.3, 0.5])


x = np.arange(len(labels))  # Label locations

width = 0.35  # Bar width


fig, ax = plt.subplots(figsize=(10, 6))

rects1 = ax.bar(x - width/2, normal, width, label='Normal Neuron')

rects2 = ax.bar(x + width/2, alzheimers, width, label='Alzheimer\'s Neuron')


# Labels and formatting

ax.set_ylabel('Relative Stability (0 to 1)')

ax.set_title('Biophysical Profile of Neurons: Normal vs Alzheimer\'s')

ax.set_xticks(x)

ax.set_xticklabels(labels)

ax.set_ylim(0, 1.1)

ax.legend()

ax.grid(axis='y', linestyle='--', alpha=0.6)


plt.tight_layout()

plt.show()







import matplotlib.pyplot as plt

import numpy as np


# Simulated data for phase shift recovery

parameters = ["Hydration (H)", "Ionic Stability (I)", "Energy (E)", "Redox Balance (R)", "Chromatin Order (C)"]

baseline = np.array([0.3, 0.4, 0.35, 0.3, 0.4])  # Alzheimer's profile

restored = np.array([0.9, 0.85, 0.95, 0.9, 0.88])  # Post-phase-shift restored neuron


# Calculate total order parameter S as average

S_baseline = np.mean(baseline)

S_restored = np.mean(restored)


# Plot 1: Phase shift required for neuron recovery

fig1, ax1 = plt.subplots(figsize=(10, 6))

x = np.arange(len(parameters))

width = 0.35

ax1.bar(x - width/2, baseline, width, label='Alzheimer Neuron', color='darkred')

ax1.bar(x + width/2, restored, width, label='Post-Phase-Shift', color='darkgreen')

ax1.set_ylabel('Normalized Parameter Value')

ax1.set_title('Phase Shift in Biophysical Parameters for Neuronal Recovery')

ax1.set_xticks(x)

ax1.set_xticklabels(parameters)

ax1.axhline(S_baseline, color='red', linestyle='--', label=f'S (Alz) = {S_baseline:.2f}')

ax1.axhline(S_restored, color='green', linestyle='--', label=f'S (Restored) = {S_restored:.2f}')

ax1.legend()

ax1.grid(True)


# Plot 2: Energy required to induce the phase shift

# Assuming arbitrary unit energy cost per parameter increase for illustration

energy_cost = (restored - baseline) * 10  # Arbitrary 10 units per parameter delta

total_energy = np.sum(energy_cost)


fig2, ax2 = plt.subplots(figsize=(10, 6))

ax2.bar(parameters, energy_cost, color='orange')

ax2.set_ylabel('Energy Input (Arbitrary Units)')

ax2.set_title(f'Total Energy Required for Phase Shift: {total_energy:.2f} Units')

ax2.grid(True)


plt.show()


Popular posts from this blog

The Death of Cancer: How to kill it.

Image
The Real Story About Cancer: What It Is, Why There’s Hope, and What You Can Actually Do 1. Cancer Isn’t Your Fault—and It Isn’t a Mystery Anymore For most people, the word “cancer” is terrifying. It can feel random, unfair, and impossible to beat. Maybe you’ve lost someone, or maybe you’re fighting it right now. Doctors often talk about genes, luck, “bad cells,” and complicated treatments that sound more like war than healing. But here’s the truth—cancer isn’t your fault. And—finally—cancer isn’t a mystery anymore. What Cancer REALLY Is Cancer happens when the environment inside your body—right down to the tiniest part of your cells—breaks down. It’s not just about “bad genes.” It’s about your cells losing their support system : the water, the oxygen, the minerals, the energy, and the calm, safe place they need to repair themselves and stay healthy. Think of your body like a beautiful garden. When it’s watered, gets sunlight, has rich soil, and is free of garbage, everything grows st...
Read more

What Is a Cell? The True Story of Life’s Smallest Wonders

Image
Introduction: The Hidden World Inside You When you look at your hand, a leaf, or even a tiny speck of pond water, you’re seeing the surface of a world made of countless living engines—cells. They’re the smallest units of life, but also the most sophisticated, mysterious, and essential. Every movement you make, every thought, every breath, every blade of grass or soaring bird—all powered by the collective work of cells. But what are cells, really? For over a century, biology textbooks have taught a simple story: cells are “bags” of molecules, each with a nucleus carrying DNA, floating in a soup of proteins and enzymes, all following the instructions of their genes. Yet that picture is more than incomplete—it’s misleading. Modern science, drawing from physics, chemistry, and cutting-edge technology, is revealing a universe where cells are not just bags of genes, but dynamic, environment-sensitive, self-organizing systems—constantly adapting, sensing, and even “deciding” their fate in res...
Read more

The Hidden Symphony: How Your DNA Really Works—and Why It Matters to Everyday Life

Image
1. A Different Way to Think About DNA When most of us hear “DNA,” we picture a tiny spiral ladder that carries genetic “instructions.” That picture is true—but it’s also wildly incomplete. Imagine describing a grand piano only as “a wooden box that stores songs.” You’d miss the hammers, the vibrating strings, the soundboard, and the music itself. DNA is more like that piano. Yes, it stores information, but it also plays that information by producing waves of energy—tiny shivers of motion and flickers of electric charge—that ripple through your cells every second of your life. Those waves organize hundreds of thousands of chemical reactions so smoothly that you never notice. Take them away and life would stall in an instant. This guide explores that hidden “musical” side of DNA in plain language. You will see why water, minerals, gentle movement, and even sunlight can change the “sound” your DNA makes—and why that matters for health, aging, and disease. 2. The Helix as a...
Read more